HOÁN VỊ - TỔ HỢP

Lý Thuyết

Giai Thừa

Trong một cuộc đua heo ở Cần Thơ, bạn được ông chủ ở đó gạ gẫm làm một kèo dự đoán thứ tự về đích của 3 chú heo tham dự trận đưa sắp diễn ra. Do mới đến, nên bạn không có thông tin về tiền sử thi đấu của các "vận động viên" này, và ông chủ cũng khẳng định không có tình huống đồng hạng xảy ra. Bạn phân vân, liệu mình có nên tham gia, và khả năng chiến thắng của mình thế nào?

Một cách thủ công, bạn loay hoay một buổi để liệt kê tất cả các trường hợp có thể xảy ra trên giấy và tính xác suất chiến thắng của mình. Sau một lúc, bạn liệt kê được 6 trường hợp có thể xảy ra và xác suất 1/6 = 16.7%. Đây có lẽ không phải là một "kèo thơm" để tham gia.

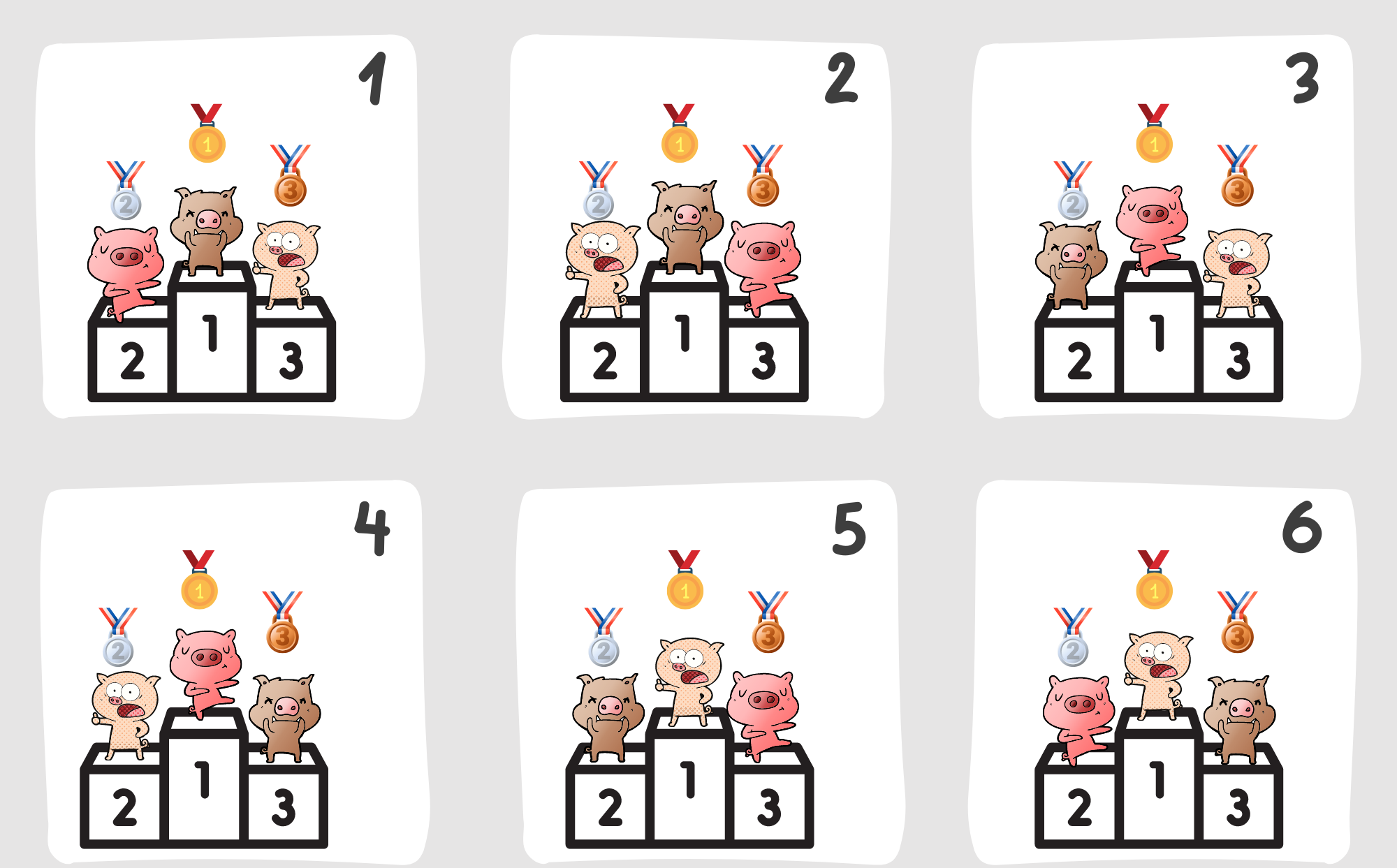
Nhưng có một vấn đề quan tâm ở đây, chỉ với 3 chú heo, bạn đã mất khá nhiều thời gian để đưa ra quyết định. Bạn tự hỏi, có cách nào để tính được trực tiếp số lượng trường hợp có thể xảy ra một cách nhanh chóng mà không cần phải ngồi liệt kê như vầy?

Hãy thử xem xét kỹ hơn từng thứ tự về đích của 3 chú heo có thể xảy ra tại cuộc đua và xem liệu có một khuôn mẫu nào ở đây không?

Có thể thấy, ta có 3 lựa chọn cho vị trí hạng nhất, và với mỗi lựa chọn đó ta lại có 2 lựa chọn vị trí hạng 2 và tương ứng là chỉ có 1 lựa chọn duy nhất cho vị trí hạng 3. Nói cách khác, số lựa chọn ta có thể có cho 3 vị trí chiến thắng là: $$\mathbf{3 \times 2 \times 1 = 6}$$ Như vậy ta đã trực tiếp tính được số lượng kết quả có thể xảy ra của cuộc đua 3 chú heo mà không cần phải liệt kê tất cả trường hợp. Giờ thì tổng quát hơn tí, nếu ta tăng số lượng "vận động viên" lên thành n, thì kết quả sẽ như thế nào: $$\mathbf{n \times (n-1) \times (n-2) \times ... \times 3 \times 2 \times 1}$$

Tuyệt vời! Với việc áp dụng cách tính trên, bạn có thể dễ dàng trực tiếp tính được số lượng cách sắp xếp của \(n\) đội tượng riêng biệt bất kỳ nào mà không cần phải liệt kê tất chúng ra. Cách tính như trên được gọi là giai thừa (factorial) của một số. Trong toán học, giai thừa được ký hiệu là đấu chấm than !. Ví dụ, giai thừa của \(3\) được viết là \(3!\) và \(n!\) là ký hiệu cho giai thừa của \(n\).

Ký hiệu giai thừa được giới thiệu lần đầu tiên vào năm 1808 bởi Christian Kramp, sau khi thấy quá dài dòng khi phải sử dụng cách viết \(\mathbf{1 \times 2 \times 3 \times 4 \times ... }\) trong các định lí hay công thức toán học. Kí hiệu \(n!\) là một cách viết ngăn gọn mang ý nghĩa "lấy tất cả các số tự nhiên từ n đến 1 và nhân chúng lại với nhau". Cụ thể: $$\mathbf{n! = n \times (n-1) \times (n-2) \times ... \times 3 \times 2 \times 1}$$

Hoán Vị

Một chỉnh hợp là một cách sắp xếp \(k\) phần tử từ \(n\) phần tử, không quan trọng thứ tự. Số lượng cách sắp xếp như vậy là \(P_{n}^{k}\), được định nghĩa như sau:

$$P_{n}^{k} = \frac{n! }{(n - k)!}$$

Tổ Hợp

Một tổ hợp là một cách sắp xếp \(k\) phần tử từ \(n\) phần tử, không quan trọng thứ tự. Số lượng cách sắp xếp như vậy là \(C_{n}^{k}\), được định nghĩa như sau:

$$C_{n}^{k} = \frac{P_{n}^{k}}{k!} = \frac{n!}{k! (n - k)!} $$

Bài Tập

• Câu 1: Từ các số 0,1,2,3,4,5 có thể lập được bao nhiêu số tự nhiên mà mỗi số có 6 chữ số khác nhau và chữ số 2 đứng cạnh chữ số 3?

  A.192 B.202 C.211 D.180

  Hướng dẫn giải

  Đáp án A

  Đặt \(x = 23\), số cần tìm sẽ có dạng \(y= abcde\). Theo đề bài ta có:

  (1) \(a, b, c, d, e\) khác nhau và thuộc tập \(\{0, 1, x, 4, 5\}\)

  (2) \( a \neq 0\) (số cần tìm có 6 chữ số);

  (3) Khi hoán đổi vị trí \(2\) và \(3\) trong \(y\) ta được hai số khác nhau (Ví dụ: \(234560\) và \(324569\)).

  \(\Rightarrow\) Từ (1), (2) và (3) ta có tổng số tự nhiên có thể có của \(y\) là: $$(P_{5} - P_{4}) \times 2 =( 120 - 24 ) \times 2 = 192$$

• Câu 2: Có 3 học sinh nữ và 2 học sinh nam. Ta muốn sắp xếp vào một bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu cách sắp xếp để 3 học sinh nữ ngồi kế nhau?

  A.34 B.46 C.36 D.26

  Hướng dẫn giải

  Đáp án C

  Đặt \(x\) là vị trí ngồi của 3 bạn nữ và \(n1\), \(n2\) tương ứng với 2 bạn nam. Cách sắp xếp cần tìm có dạng \(y= abc\). Trong đó \(a, b, c\) khác nhau và thuộc tập \(\{x, n1, n2\}\).

  (1) Ta có số cách sắp xếp có thể có của \(y = P_{3} = 3! = 6\)

  (2) Tương tự ta có cách sắp xếp 3 bạn nữ trong \(x = P_{3} = 3! = 6\)

  \(\Rightarrow\) Từ (1) và (2) ta có tổng số cá sắp xếp có thể có là: \(6 \times 6 = 36\)

Post Tags Giai thừa Tổ hợp Chính hợp Toán